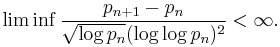Landau's problems

At the 1912 International Congress of Mathematicians, Edmund Landau listed four basic problems about primes. These problems were characterised in his speech as "unattackable at the present state of science" and are now known as Landau's problems. They are as follows:

  1. Goldbach's conjecture: Can every even integer greater than 2 be written as the sum of two primes?
  2. Twin prime conjecture: Are there infinitely many primes p such that p + 2 is prime?
  3. Legendre's conjecture: Does there always exist at least one prime between consecutive perfect squares?
  4. Are there infinitely many primes p such that p − 1 is a perfect square? In other words: Are there infinitely many primes of the form n2 + 1? (sequence A002496 in OEIS).

As of 2011, all four problems are unresolved.

Contents

Progress toward solutions

Goldbach's conjecture

Vinogradov's theorem proves Goldbach's weak conjecture for sufficiently large n. Deshouillers, Effinger, te Riele and Zinoviev conditionally proved the weak conjecture under the GRH.[1] The weak conjecture is known to hold for all n outside the range 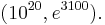(10^{20}, e^{3100}).[1][2]

Chen's theorem proves that for all sufficiently large n, 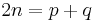2n=p%2Bq where p is prime and q is either prime or semiprime. Montgomery and Vaughan showed that the exceptional set (even numbers not expressible as the sum of two primes) was of density zero.[3]

Twin prime conjecture

Goldston, Pintz and Yıldırım showed that the size of the gap between primes could be far smaller than the average size of the prime gap:

\liminf\frac{p_{n%2B1}-p_n}{\sqrt{\log p_n}(\log\log p_n)^2}<\infty.[4]

Earlier, they conditionally proved a weaker version of the twin prime conjecture, that infinitely many primes p exist with 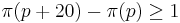\pi(p%2B20)-\pi(p)\ge1, under the Elliott–Halberstam conjecture.[5] 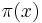\pi(x) is the prime-counting function. The twin prime conjecture replaces 20 with 2.

Chen showed that there are infinitely many primes p (later called Chen primes) such that p+2 is either a prime or a semiprime.

Legendre's conjecture

It suffices to check that each prime gap starting at p is smaller than 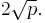2\sqrt p. A table of maximal prime gaps shows that the conjecture holds to 1018.[6] A counterexample near 1018 would require a prime gap fifty million times the size of the average gap.

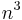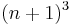A result due to Ingham shows that there is a prime between n^3 and (n%2B1)^3 for every large enough n.[7]

Near-square primes

The Friedlander–Iwaniec theorem shows that infinitely many primes are of the form 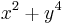x^2%2By^4.

Iwaniec showed that there are infinitely many numbers of the form 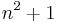n^2%2B1 with at most two prime factors.[8]

Notes

  1. ^ a b Deshouillers, Effinger, Te Riele and Zinoviev, "A complete Vinogradov 3-primes theorem under the Riemann hypothesis", Electronic Research Announcements of the American Mathematical Society 3, pp. 99-104 (1997).
  2. ^ Liu, M. C.; Wang, T. Z. (2002). "On the Vinogradov bound in the three primes Goldbach conjecture". Acta Arithmetica 105: 133–175. doi:10.4064/aa105-2-3. 
  3. ^ Montgomery, H. L.; Vaughan, R. C. (1975). "The exceptional set in Goldbach's problem". Acta Arithmetica 27: 353–370. http://matwbn.icm.edu.pl/ksiazki/aa/aa27/aa27126.pdf. 
  4. ^ Daniel Alan Goldston, Yoichi Motohashi, János Pintz and Cem Yalçın Yıldırım, Primes in tuples. II. Preprint.
  5. ^ Daniel Alan Goldston, Yoichi Motohashi, János Pintz and Cem Yalçın Yıldırım, Small Gaps between Primes Exist. Proceedings of the Japan Academy, Series A Mathematical Sciences 82 4 (2006), pp. 61-65.
  6. ^ Jens Kruse Andersen, Maximal Prime Gaps
  7. ^ Ingham, A. E. (1937). "On the difference between consecutive primes". Quarterly Journal of Mathematics Oxford 8 (1): 255–266. doi:10.1093/qmath/os-8.1.255. 
  8. ^ Iwaniec, H. (1978). "Almost-primes represented by quadratic polynomials". Inventiones Mathematicae 47 (2): 178–188. doi:10.1007/BF01578070. 

External links